Malgré l'importance croissante des modèles DSGE non linéaires, leur estimation est encore très limitée, principalement en raison de la charge de calcul élevée associée aux techniques d'estimation non linéaires. En outre, certains problèmes d'identification peuvent se poser en raison des non-régularités découlant de la solution non linéaire.
Existe-t-il des méthodes d'estimation qui permettent de surmonter ces problèmes et facilitent l'application de l'estimation DSGE non linéaire ? Les versions bayésiennes des méthodes des moments peuvent apporter une réponse utile en ce sens. En particulier, cet article préconise l'utilisation de l'Approximate Bayesian Computation, un ensemble de techniques développées en épidémiologie et en génétique des populations (Pritchard et al.[2000]).
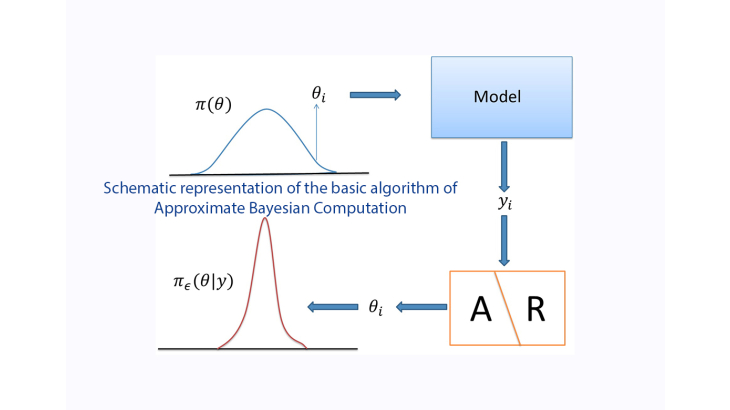
L'ABC est un ensemble de méthodes bayésiennes par lesquelles la distribution préalable des paramètres structurels du modèle est mise à jour par les informations fournies par les moments (variances, covariances, etc.). Dans un premier temps, un grand nombre de vecteurs de paramètres est tiré de la distribution précédente. Dans une deuxième étape, pour chaque vecteur ou paramètre, le modèle est simulé. Pour chaque simulation, la distance entre le vecteur des moments simulés et le vecteur des moments observés est calculée. Dans une troisième étape, une étape de sélection est effectuée pour chaque simulation : les simulations ne sont acceptées que si la distance euclidienne est inférieure à un seuil fixe, sinon elles sont rejetées. Enfin, les paramètres associés aux simulations acceptées fournissent une approximation de la distribution postérieure.
Grâce aux exercices de Monte Carlo, je montre que l'ABC a une meilleure performance des petits échantillons par rapport à la méthode bayésienne de pointe des moments utilisés dans l'estimation DSGE, la Bayesian Limited Information (Kim[2002], Christiano et al. Ce résultat dépend de la manière dont la distribution des moments est obtenue et utilisée pour mettre à jour la distribution précédente.
De plus, j'estime un modèle DSGE néo-keynésien avec un ZLB parfois contraignant en utilisant une simple version de l'ABC (ABC-rejection). J'estime le modèle sur les données américaines en utilisant ABC et je trouve trois résultats. Premièrement, l'inclusion de la période de la ZLB dans l'échantillon est cruciale pour estimer correctement la probabilité d'atteindre la limite inférieure de zéro. Deuxièmement, l'utilisation de moments conditionnels dans l'estimation (c.-à-d. des moments conditionnels à l'état de l'économie) peut atténuer les problèmes d'identification générés par la présence de la borne inférieure zéro. Troisièmement, l'estimation aide le modèle à reproduire certaines des principales caractéristiques observées avant et après la Grande Récession et à faciliter la sur-réaction des variables macroéconomiques prédites par le DSGE avec ZLB, comme le souligne Fernandez-Villaverde[2015].