Une approche unifiée des conditions de détermination dans les modèles à changement de régimes

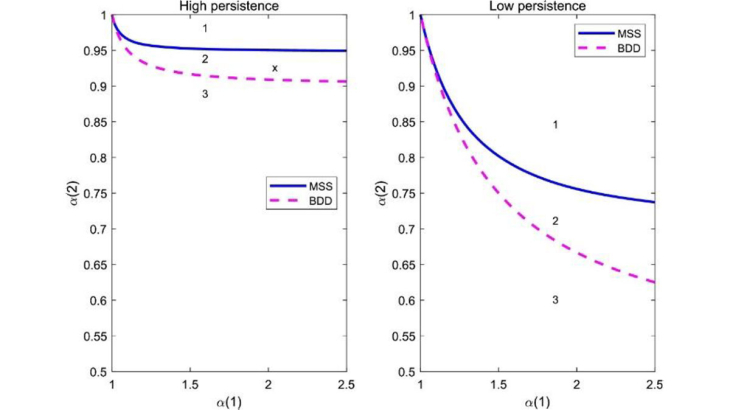
Document de travail n°972. Les conditions qui garantissent l’existence d’un équilibre stable unique – conditions de détermination- pour des modèles à anticipations rationnelles avec des changements de régime markoviens dépendent du concept de stabilité, à la différence des modèles linéaires à anticipations rationnelles. Dans ce papier, nous proposons un cadre unifié pour les deux concepts de stabilité usuellement utilisés : l’espace des processus bornés et celui des processus à espérance et variance bornées (mean-square stable). Nous exprimons les conditions de détermination pour ces deux concepts à l’aide de métriques matricielles simples. Nous montrons que les solutions à espérance et variance bornées sont toujours plus nombreuses que les solutions bornées. Nous appliquons et discutons nos résultats pour deux modèles monétaires.