Billet n°150. La règle de Taylor fournit un parangon naturel du taux d’intérêt nominal à court terme, bien que sujet à une incertitude considérable. Ce billet quantifie cette incertitude et montre l’apport de cette quantification au diagnostic de politique monétaire. Il en ressort qu’en 2019 le taux d’intérêt à court terme en zone euro s’est situé proche du milieu de l’intervalle de référence ainsi obtenu.
Le taux de Taylor : un point de comparaison fréquemment utilisé
Le taux d’intérêt prescrit par la règle de Taylor (1993) constitue le point de référence le plus fréquemment utilisé pour juger du niveau des taux d’intérêt nominaux. De quoi s’agit-il ? La règle de Taylor est une relation décrivant le taux d’intérêt de court terme désiré comme une fonction (i) de l’écart de l’inflation à sa cible, (ii) d’une mesure d’activité (par exemple, l’écart de la production à son niveau potentiel ou l’écart du chômage à son niveau "naturel") et (iii) du taux d’intérêt réel dit "neutre". Sur ce point, voir Garnier, Lhuissier et Penalver (2019).
Cette règle fournit une description positive de la politique monétaire : elle décrit ce qui a été fait. Mais sous certaines conditions, elle offre aussi une recommandation normative : elle dit ce qu’il faudrait faire. C’est à ce titre qu’elle est souvent utilisée comme la référence à laquelle on devrait comparer le niveau du taux d’intérêt nominal de court terme. Si ce dernier est inférieur (resp. supérieur) au niveau prescrit par la règle de Taylor, la politique monétaire est jugée accommodante (resp. restrictive).
La question n’est donc pas de savoir si les taux d’intérêt sont trop bas ou trop élevés dans l’absolu mais plutôt de savoir s’ils sont au-dessus ou au-dessous du niveau prescrit par la règle de Taylor.
Mais une référence entourée d’une grande incertitude
Cette question pose toutefois plusieurs problèmes pratiques.
- Quelle est la spécification correcte de la règle de Taylor ? Il existe des dizaines de formulations alternatives, selon que l’on utilise le glissement annuel des prix ou leur variation trimestrielle, que l’on considère la valeur contemporaine ou la valeur anticipée des variables, que l’on intègre une mesure du taux neutre variable ou non et selon la définition de la mesure d’activité. D’une spécification à l’autre, le diagnostic de politique monétaire peut changer considérablement.
- Quelles sont les valeurs des paramètres de la règle de Taylor ? À supposer que l’on connaisse la bonne spécification de cette dernière, les valeurs de ses paramètres doivent être estimées et sont donc sujettes à une incertitude statistique. Là encore, le diagnostic de politique monétaire sera modifié selon que la règle réagisse plus ou moins vigoureusement à l’écart de l’inflation à sa cible.
- Et même à supposer qu’on connaisse la bonne spécification et les valeurs des paramètres de la règle de Taylor, reste à savoir comment mesurer les variables d’activité économique que la règle de Taylor intègre mais qu’on n’observe pas directement (par exemple, l’écart de production ou le taux neutre) ?
Sur chacune de ces dimensions, le niveau du taux de Taylor est sujet à une incertitude considérable, comme pour n’importe quel diagnostic macroéconomique. En paraphrasant Christopher Sims, prix Nobel d’Économie en 2011, la tâche qui incombe aux économistes est de caractériser la distribution de probabilités autour de ce niveau.
Intégrer cette incertitude dans le diagnostic de politique monétaire
La formulation correcte d’un diagnostic de politique monétaire doit donc intégrer l’incertitude qui entoure le taux de Taylor. Mais comment faire en pratique ?
L’approche proposée ici consiste d’abord à se munir de 200 spécifications possibles de la règle de Taylor, couvrant largement le champ des règles considérées dans la littérature depuis l’article de Taylor. Ces règles sont ensuite combinées avec une représentation simplifiée de l’économie de la zone euro, composée d’une courbe de demande (une courbe investissement-épargne ou courbe IS) et d’une courbe d’offre (une courbe de Phillips). Ces deux courbes servent à identifier les variables inobservables (production naturelle, taux neutre).
Toutes ces relations combinées forment 200 modèles macro-économétriques qu’on estime. L’étape d’estimation permet de caractériser (1) les distributions de probabilités des différents modèles ; (2) conditionnellement à un modèle, les distributions de probabilités des paramètres des différentes règles de Taylor ; et (3) conditionnellement à un modèle et à des valeurs pour ses paramètres, les distributions de probabilités des variables inobservables.
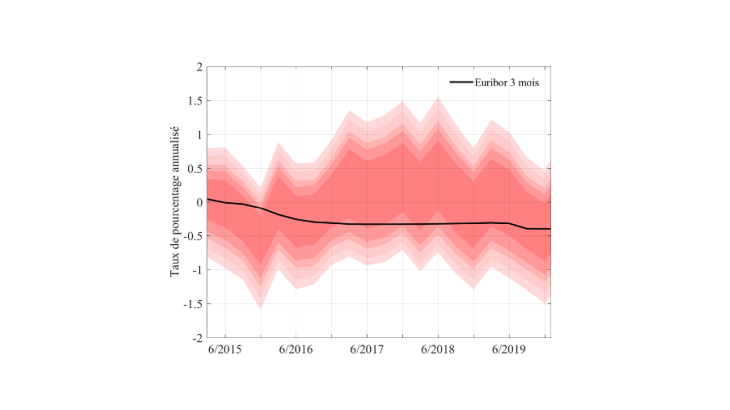
En combinant ces distributions, on aboutit à une caractérisation de l’incertitude entourant le taux de Taylor. Elle est représentée sur le graphique 1, sur la période 2014-2019. Le trait noir correspond à l’Euribor 3 mois, pris ici comme le taux d’intérêt de court terme pertinent. Les zones en rose, du plus foncé au plus clair, correspondent aux intervalles de confiance à 50%, 70% 80%, 90% et 95% des taux de Taylor.
En 2019, le taux d’intérêt à court terme en zone euro s’est situé proche du milieu de la distribution de probabilités des taux de Taylor
A de très rares exceptions près (comme fin 2015, juste avant la baisse du taux directeur de la BCE en mars 2016), l’Euribor 3 mois se situe dans l’intervalle à 50% des taux de Taylor (la zone en rose foncé). En particulier, sur l’année 2019, le taux d’intérêt de court terme se place presque dans le milieu de l’intervalle à 50%, notamment après la baisse du taux de la facilité de dépôt de l’Eurosystème décidée en septembre 2019 (compte tenu de l’orientation à la baisse de la distribution des taux de Taylor au cours de l’année).
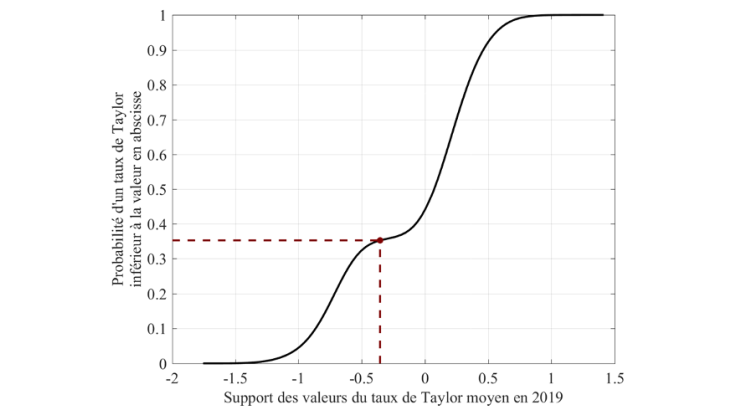
Une autre façon de formuler ce diagnostic de politique monétaire consiste à représenter la distribution des taux de Taylor (moyens) sur une année donnée. C’est ce que montre le graphique 2 pour 2019. La courbe noire représente la probabilité que le taux de Taylor soit inférieur à la valeur en abscisse. Par exemple, en 2019, la probabilité d’un taux de Taylor inférieur à -1,7% est de zéro tandis que celle d’un taux de Taylor inférieur à 1,5% est de 1. L’abscisse du rond rouge correspond au niveau moyen sur 2019 de l’Euribor 3 mois.
Le taux de Taylor sur 2019 a une probabilité d’environ 35% d’être inférieur à l’Euribor 3 mois moyen. Dit autrement, 35% des taux de Taylor se situent sous le niveau moyen de l’Euribor 3 mois en 2019, ce qui suggère en moyenne sur l’année des conditions monétaires très légèrement accommodantes comparativement à la distribution des taux de Taylor.
