Working Paper Series no. 1027. The popular choice of using a direct forecasting scheme implies that the individual predictions ignore information on their cross-horizon dependence. However, this dependence is needed if the forecaster has to construct, based on direct density forecasts, predictive objects that are functions of several horizons (e.g. when constructing annual-average growth rates from quarter-on-quarter growth rates). To address this issue, we propose to use copulas to combine the individual h-step-ahead predictive distributions into a joint predictive distribution. Our method is particularly appealing to practitioners for whom changing the direct forecasting specification is too costly. In a Monte Carlo study, we demonstrate that our approach leads to a better approximation of the true density than an approach which ignores the potential dependence. We show the superior performance of our method in several empirical examples, where we construct (i) quarterly forecasts using month-on-month direct forecasts, (ii) annual-average forecasts using monthly year-on-year direct forecasts, and (iii) annual-average forecasts using quarter-on-quarter direct forecasts.
Scores for density forecasts: “dependence-attentive” vs “dependence-inattentive”
Non-Technical Summary
Forecasting has become increasingly probabilistic, with central banks and research institutions routinely relying on density forecasts that characterize the full distribution of possible outcomes for key economic variables. In practice, however, multi-horizon forecasts are typically produced for short-term changes in the target variable (such as month-on-month or quarter-on-quarter growth rates), whereas users often require predictions for aggregated, calendar-consistent, horizons, including annual average or year-on-year growth rates. When the input densities are combined by a “dependence-inattentive” forecaster, the resulting predictive distributions fail to account for the serial-dependence that naturally arises across successive periods. Consequently, uncertainty is systematically underestimated, particularly in the tails of the distribution, precisely where policymakers’ interests frequently lie.
To address this problem, this paper develops a general methodology for transforming individual marginal predictive densities into coherent aggregated forecasts while explicitly capturing the serial-dependence across horizons. The approach relies on copulas, i.e. multivariate cumulative distribution functions that reconcile the marginal densities with a dependence structure, where the correlation parameters are estimated from historical forecast errors using the probability-integral transforms of realized outcomes. Incorporating this dependence allows the “dependence-attentive” forecaster to simulate the full joint distribution and, in turn, to construct predictive densities for any aggregated target variable, such as annual average growth rates derived from quarter-on-quarter growth forecasts.
The proposed methodology is intentionally simple, model-agnostic, and practical. It can be implemented using existing forecasts without altering the underlying econometric models. As a result, forecasters can enhance the accuracy and coherence of their risk assessments across horizons while preserving their established forecasting frameworks.
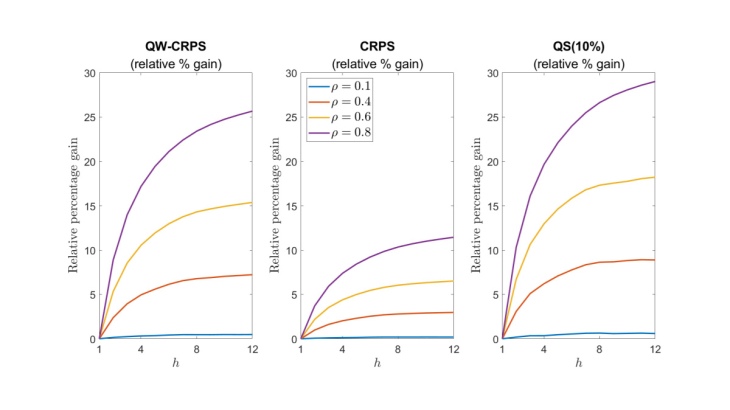
The paper evaluates this new approach using both Monte Carlo experiments and empirical applications. The simulation results demonstrate that incorporating cross-horizon dependence yields better forecasting, with more accurate predictive densities, especially when the underlying economic variables exhibit persistence or when the aggregation spans multiple periods. The improvements are particularly pronounced for scoring rules that place greater weight on tail accuracy, measures that are central in risk management.
Three empirical exercises are presented in the figure below in order to further illustrate the method’s practical value. First, using a large-scale set of bivariate regressions with US data from the FRED-MD database, density forecasts for month-on-month growth rates are transformed into quarter-on-quarter growth rates. Second, monthly density forecasts of year-on-year US inflation are converted into annual-average predictive distributions. Third, annual-average densities of US GDP growth are obtained from quarterly predictive distributions. In all cases, the copula-based approach consistently outperforms benchmarks that assume independence across horizons, as measured by the difference between the “dependence attentive” forecaster (who implements our proposed methodology) and the “dependence inattentive” (who does not).
The findings underscore three key messages. First, ignoring serial dependence across forecast horizons leads to a systematic underestimation of risk and uncertainty. Second, the proposed copula-based transformation offers a practical and cost-effective means of correcting this deficiency without the need to redesign existing forecasting models. Third, the largest gains arise for tail-sensitive and long-horizon applications, which are particularly relevant for policy analysis under uncertainty.
Overall, the study provides a robust and easy-to-implement framework for transforming density forecasts into new target distributions. By more accurately capturing joint uncertainty across time, the approach enhances both the reliability and the policy usefulness of probabilistic forecasts.
Keywords: Joint Predictive Distribution, Frequency Transformation, Path Forecasts, Cross-horizon Dependence.
Codes JEL : C53, C32, E37
Download the full publication
Updated on the 23rd of December 2025