Working Paper Series no. 936. How can a central bank avoid losing control over inflation expectations in the face of a large supply shock ? Under rational expectations, respecting the Taylor principle - increasing rates more than one for one with inflation - prevents self-fulfilling inflation and defines an active monetary policy. We reconsider the issue away from rational expectations, for a large class of boundedly rational expectations featuring both limited foresight and long-term learning. We show three results. (1) When restricting monetary policy to a Taylor rule, the Taylor principle does not prevent self-fulfilling inflation but hyperinflation spirals, unless for unrealistically high degrees of foresight. (2) Against hyperinflation spirals, active monetary policy can be characterized without restricting policy to a Taylor rule, as a sufficient increase of a weighted average of present and future expected policy rates. (3) The weights on future policy rates first increase but then decrease with the horizon, implying that delaying hikes too much requires larger hikes later, with a larger drop in output. Yet, being slow in hiking rates can be optimal provided a large cost on output stabilization, as it spreads the output cost over time.
How can a central bank avoid losing control over inflation expectations in the face of a large supply shock? The question has come back front and center following the Covid pandemic, as the world economy experienced supply shocks and inflation levels of magnitude not seen in 40 years. Standard monetary models provide a well-known response to this question: Respecting the Taylor principle - i.e. increasing interest rates more than one-for-one with inflation - prevents inflation from becoming self-fulfilling and defines an active monetary policy. The last worldwide episode of high inflation- the Great Inflation of the 1970s - has been linked to central banks' failure to respect the Taylor principle.
In standard models, the need to respect the Taylor principle is derived under the assumption of rational expectations. In this paper, we revisit the question of how to keep control over inflation expectations when they are instead boundedly rational.
What motivates us to move away from rational expectations is that the Taylor principle is actually only necessary to prevent self-fulfilling inflation in baseline New-Keynesian models. But baseline New-Keynesian models find forward guidance (FG) to have unrealistically large effects on inflation and output - the FG puzzle. Solutions to the FG puzzle mainly work by adding discounting to baseline models. Yet, when adding enough discounting to solve the FG puzzle, a unique equilibrium with no self-fulfilling inflation obtains even under an interest-rate peg - a fully passive monetary policy. This would suggest that the need to adopt a sufficiently active monetary policy - to increase rates sufficiently in response to an inflationary shock - is an artifact of unrealistically forward-looking models.
We move away from rational expectations and rely on Woodford (2019)'s model of bounded rationality which combines two forms of bounded rationality: finite planning horizons and long-term learning. Finite planning horizons make expectations less forward-looking than rational expectations, providing a solution to the FG puzzle. Long-term learning makes expectations about the long run backward-looking. We show three results.
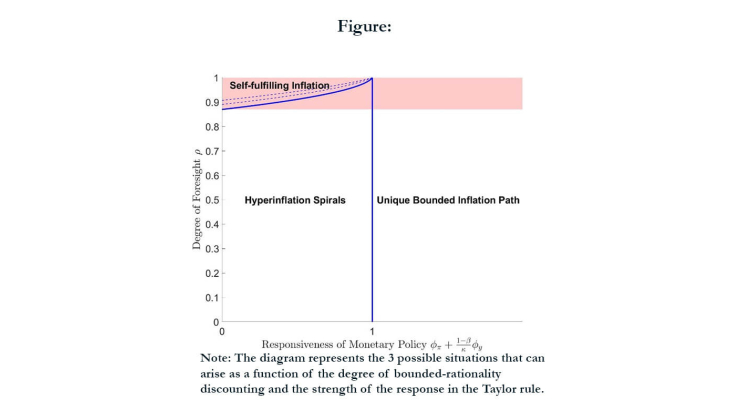
First, we show that except for unrealistically high degrees of foresight, active monetary policy prevents hyperinflation spirals and not self-fulfilling inflation. Assuming the central bank sets interest rates by following a Taylor rule, we show that the Taylor principle remains necessary and sufficient for a unique bounded solution. However, this Taylor principle prevents self-fulfilling inflation only for very high degrees of foresight for which the model runs into the FG puzzle. Whenever foresight is low enough to avoid the FG puzzle, the Taylor principle prevents instead the risk that the economy go on an hyperinflation path, as long-run inflation expectations gradually de-anchor.
Second, we move beyond Taylor rules. We characterize all the exogenous interest rate paths that ensure a determinate bounded equilibrium where inflation returns to its target in the long run. The characterization states that a weighted average of present and future expected policy rates must increase sufficiently. We use the characterization to define the relative anchoring effect of a rate hike at a given horizon: how much it brings down inflation in the long run, relative to a contemporaneous interest rate hike. We show that the relative anchoring effect is the highest at intermediary horizons. Delaying hikes beyond the first few quarters therefore requires to hike them more tomorrow.
Finally, we derive the optimal monetary policy response to a cost-push shock. The more weight the central bank puts on output, the less the central bank should increase rates on impact, avoiding a fall in output today. While not increasing rates today requires to increase them more later, it does not follow that increasing rates slowly only sets the stage for a worse recession tomorrow. Provided rates are then kept high, increasing rates slowly can be justified by a large weight on output stabilization, in order to spread the output cost across time.